DAY 22 試題

問題描述

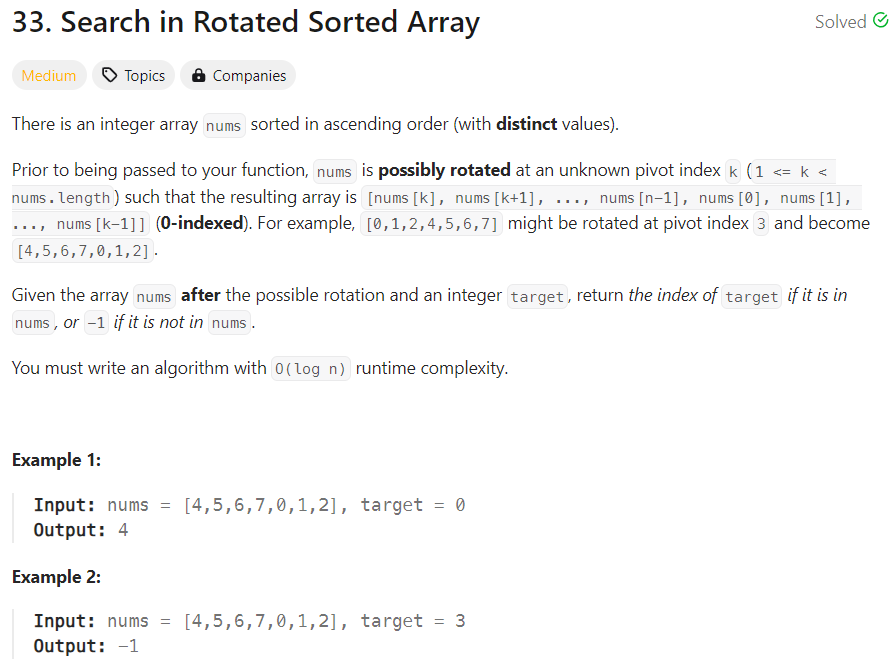
給定一個升序排列的整數陣列 nums，該陣列可能在未知的樞軸點進行了旋轉，例如 [0,1,2,4,5,6,7] 可能在樞軸點 3 旋轉後變為 [4,5,6,7,0,1,2]。要求在此旋轉過的陣列中找到目標數字 target 的索引。如果目標數字存在於陣列中，返回其索引；否則，返回 -1。

要求使用時間複雜度為 O(log n) 的演算法來解決問題。

範例 1：

• 輸入：nums = [4,5,6,7,0,1,2], target = 0
• 輸出：4
• 解釋：目標數字 0 位於索引 4。

範例 2：

• 輸入：nums = [4,5,6,7,0,1,2], target = 3
• 輸出：-1
• 解釋：目標數字 3 不在陣列中。

範例 3：

• 輸入：nums = [1], target = 0
• 輸出：-1
• 解釋：目標數字 0 不在陣列中。

解題思路

要在旋轉過的排序陣列中找到目標數字，可以利用二分搜尋法，因為陣列的兩部分仍然是局部有序的。具體步驟如下：

1. 初始化指標：設置 left 指向陣列的開頭，right 指向陣列的末尾。

2. 二分搜尋：

• 計算中間位置 mid。
• 如果 nums[mid] == target，直接返回 mid。
• 判斷哪一部分是有序的：
  • 如果 nums[left] <= nums[mid]，表示左半部分是有序的：
    • 如果 target 在左半部分的範圍內，則調整 right 指標。
    • 否則，調整 left 指標。
  • 否則，右半部分是有序的：
    • 如果 target 在右半部分的範圍內，則調整 left 指標。
    • 否則，調整 right 指標。

3. 結束條件：當 left 超過 right 時，如果還未找到目標數字，則返回 -1。

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0, right = nums.size() - 1;
        
        while (left <= right) {
            int mid = left + (right - left) / 2;
            
            // 如果找到目標數字，返回其索引
            if (nums[mid] == target) {
                return mid;
            }
            
            // 左半部分是有序的
            if (nums[left] <= nums[mid]) {
                // 目標數字在左半部分
                if (nums[left] <= target && target < nums[mid]) {
                    right = mid - 1;
                } else {  // 否則目標數字在右半部分
                    left = mid + 1;
                }
            }
            // 右半部分是有序的
            else {
                // 目標數字在右半部分
                if (nums[mid] < target && target <= nums[right]) {
                    left = mid + 1;
                } else {  // 否則目標數字在左半部分
                    right = mid - 1;
                }
            }
        }
        
        // 如果沒有找到目標數字，返回 -1
        return -1;
    }
};

解法重點與分析

1. 二分搜尋法的應用：雖然陣列被旋轉過，但仍可利用二分搜尋法的特性，只需判斷左右兩邊是否有序，即可決定搜索的區間。
2. 有序區間的判斷：在每次迭代中，通過比較 nums[left] 和 nums[mid]，可以確定哪一部分是有序的，然後根據 target 的範圍來縮小搜索範圍。
3. 時間複雜度：O(log n)。二分搜尋法每次將搜索範圍縮小一半，因此能夠在對數時間內完成搜索。
4. 空間複雜度：O(1)，只需要常數額外空間來存儲指標和變數。

總結

這道題透過二分搜尋法在旋轉過的排序陣列中找到目標數字。解法利用旋轉陣列的特性，通過判斷左右兩邊是否有序來決定搜索的方向。由於二分搜尋法的高效性，該解法能夠在 O(log n) 時間內找到目標數字。

以上是第二十二天的自學內容分享，謝謝大家。